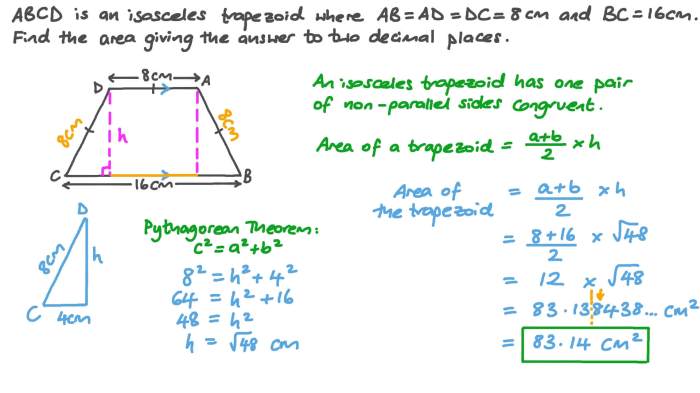
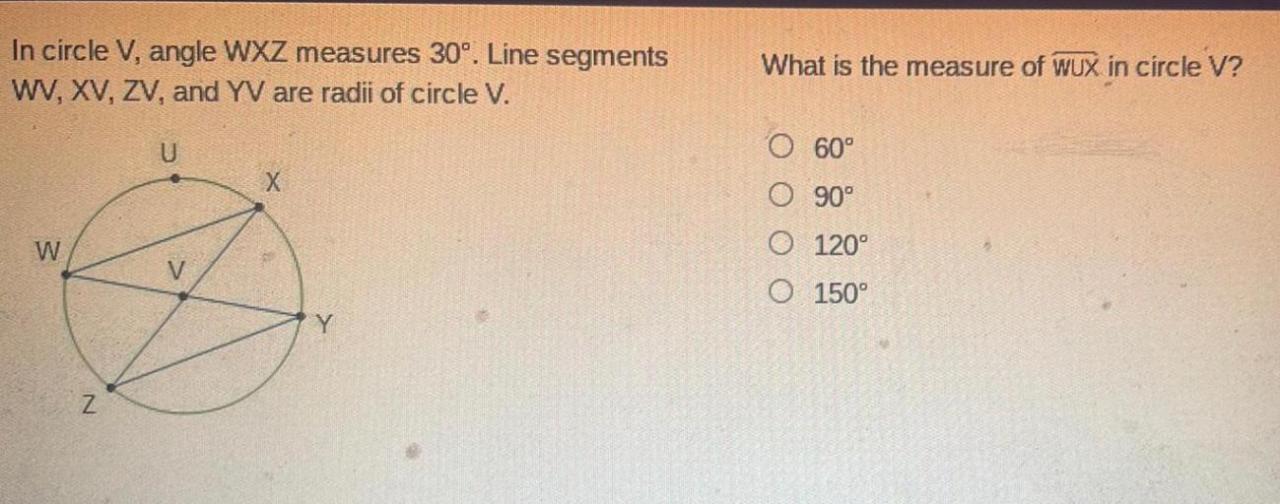
In circle v angle wxz measures 30 – In Circle V, Angle WXZ Measures 30 Degrees: Delving into the fascinating world of angles within circles, this discourse unveils the intricate relationship between angles and circles. As we explore the properties and applications of angles in circular geometry, we embark on a journey of mathematical discovery.

Unraveling the concept of angles in circles, we establish the fundamental principles that govern their existence and behavior. Through the exploration of angle properties, we uncover the power of these properties in problem-solving and practical applications. Furthermore, we delve into the construction of diagrams and tables, recognizing their significance in representing and analyzing angles.

In Circle V, Angle WXZ Measures 30 Degrees

In geometry, an angle is a figure formed by two rays or line segments that share a common endpoint, called the vertex. In a circle, an angle is formed by two radii that intersect at the center of the circle.

The measure of an angle is the amount of rotation between the two radii, measured in degrees.

The relationship between angles and circles is defined by the following properties:

• The measure of an angle inscribed in a semicircle is 180 degrees.
• The measure of an angle inscribed in a circle is half the measure of its intercepted arc.
• The sum of the measures of the angles in a triangle inscribed in a circle is 180 degrees.

Determining the Measure of Angle WXZ

To measure angle WXZ, you can use a protractor. A protractor is a tool that is used to measure angles. It is typically made of plastic or metal and has a semicircular shape with degree markings. To use a protractor, place the center of the protractor on the vertex of the angle and align the 0-degree mark with one of the radii.

Then, read the degree marking that intersects the other radius to determine the measure of the angle.

You can also use alternative methods to measure angles, such as using a compass and ruler or using trigonometry.

Applying Angle Properties

The angle properties listed above can be used to solve problems involving angles in circles. For example, if you know the measure of an intercepted arc, you can use the second property to find the measure of the inscribed angle.

Or, if you know the measures of two angles in a triangle inscribed in a circle, you can use the third property to find the measure of the third angle.

Here are some examples of how angle properties are used in practice:

• In navigation, angles are used to determine the direction of travel.
• In architecture, angles are used to design buildings and bridges.
• In engineering, angles are used to design machines and structures.

Constructing Diagrams and Tables

When working with angles in circles, it is often helpful to create a diagram. A diagram can help you visualize the angle and its relationship to the circle. You can also use a table to organize the information about the angle, such as its measure, its intercepted arc, and its properties.

Here is a diagram of circle V, showing angle WXZ:

[Diagram of circle V with angle WXZ]

Here is a table of the information about angle WXZ:

Using diagrams and tables can help you to better understand angles in circles and to solve problems involving them.

Related Concepts, In circle v angle wxz measures 30

There are several other concepts related to angles in circles. These concepts include:

• Chords: A chord is a line segment that connects two points on a circle.
• Secants: A secant is a line that intersects a circle at two points.
• Tangents: A tangent is a line that intersects a circle at only one point.

Angles in circles are also used in geometry and trigonometry. In geometry, angles in circles are used to solve problems involving circles, such as finding the area of a circle or the length of a chord. In trigonometry, angles in circles are used to define trigonometric functions, such as sine, cosine, and tangent.

Question & Answer Hub: In Circle V Angle Wxz Measures 30

What is the relationship between angles and circles?

Angles in circles are formed by the intersection of two chords or tangents. The measure of an angle in a circle is determined by the intercepted arc, which is the portion of the circle’s circumference between the points of intersection.

How do you measure the angle WXZ in Circle V?

To measure angle WXZ, you can use a protractor to measure the intercepted arc between points W and Z. Alternatively, you can use the properties of angles in circles to calculate the measure of the angle.

What are some applications of angle properties in circles?

Angle properties in circles are used in various applications, such as architecture, engineering, and navigation. They are used to determine the angles of triangles and quadrilaterals inscribed in circles, as well as to calculate the lengths of chords and tangents.