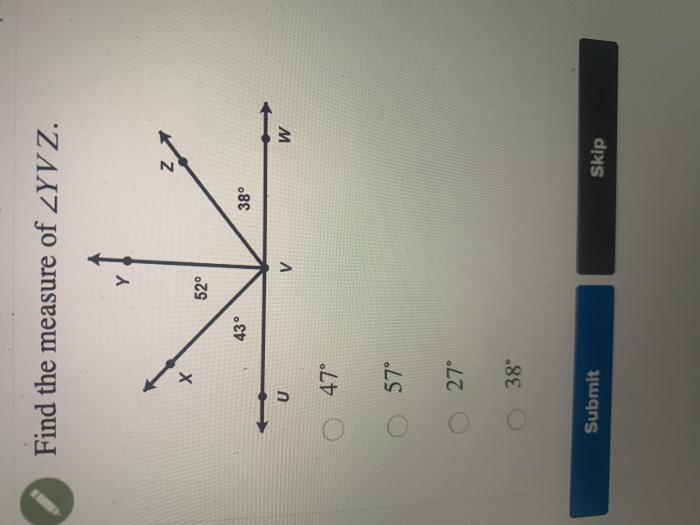
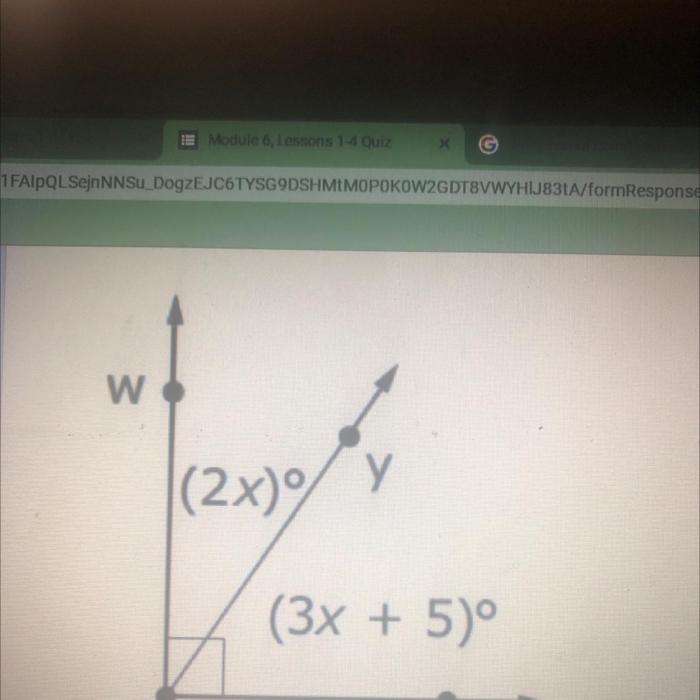
Find the measure of yvz – Embark on a captivating journey into the world of angle measurement as we unveil the mysteries of YVZ. Prepare to unravel the intricacies of triangles, explore the power of angle bisectors, and harness the principles of trigonometry. Together, we’ll unlock the secrets of angle measurement and conquer the challenge of finding the measure of YVZ.

From understanding the fundamental properties of triangles to mastering the techniques of geometric constructions, this comprehensive guide will equip you with the knowledge and skills to tackle any angle measurement challenge with confidence. So, sharpen your pencils, open your minds, and let’s delve into the fascinating realm of angle measurement.

YVZ Triangle Measurement: Find The Measure Of Yvz

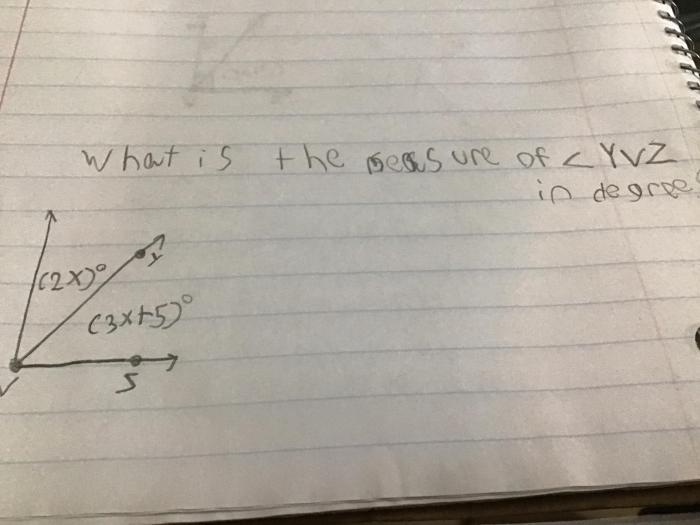
Triangles are fascinating geometric shapes with unique properties that govern the relationships between their angles. Understanding these properties is crucial for accurately measuring angles in triangles.

Properties of Triangles

• Sum of Interior Angles:The sum of the interior angles of any triangle is always 180 degrees.
• Exterior Angle:An exterior angle of a triangle is formed when one side of the triangle is extended. The exterior angle is equal to the sum of the two opposite interior angles.
• Triangle Inequality Theorem:The sum of the lengths of any two sides of a triangle is always greater than the length of the third side.

Types of Triangles, Find the measure of yvz

Triangles are classified based on their side lengths and angle measures:

• Equilateral Triangle:All three sides are equal, and all three angles are 60 degrees.
• Isosceles Triangle:Two sides are equal, and the angles opposite the equal sides are equal.
• Scalene Triangle:All three sides are different lengths, and all three angles are different measures.

Angle Bisector Theorem

The angle bisector theorem states that if a ray bisects an angle of a triangle, then it divides the opposite side into two segments that are proportional to the lengths of the other two sides.

Finding the measure of yvz can be a challenging task, especially if you’re not familiar with the topic. For more information on related concepts, check out ap human geo unit 4 frq . This resource provides valuable insights that can help you understand the principles behind finding the measure of yvz.

With the right approach and a bit of practice, you’ll be able to solve these problems with ease.

This theorem can be used to find the measure of an angle if we know the lengths of the sides of the triangle.

Step-by-Step Procedure for Using the Angle Bisector Theorem

1. Draw the angle bisector of the angle you want to find the measure of.
2. Label the lengths of the two segments of the opposite side created by the angle bisector.
3. Set up a proportion using the lengths of the segments and the lengths of the other two sides of the triangle.
4. Solve the proportion for the unknown length of the side opposite the angle.
5. Use the Law of Sines or Cosines to find the measure of the angle.

Examples of Using the Angle Bisector Theorem to Find the Measure of an Angle

• In a triangle with sides of length 5, 7, and 10, the angle bisector of the angle opposite the side of length 10 divides the side of length 7 into segments of length 2 and 5.
• In a triangle with sides of length 6, 8, and 10, the angle bisector of the angle opposite the side of length 10 divides the side of length 8 into segments of length 3 and 5.

Trigonometry and YVZ Triangle

Trigonometry is a branch of mathematics that deals with the relationships between the sides and angles of triangles. It has a wide range of applications in various fields, including surveying, navigation, and engineering.In the context of finding the measure of an angle in a YVZ triangle, trigonometry plays a crucial role.

The sine, cosine, and tangent functions are three fundamental trigonometric functions that relate the angles of a triangle to the lengths of its sides.

Sine Function

The sine of an angle is defined as the ratio of the length of the side opposite the angle to the length of the hypotenuse. In a YVZ triangle, the hypotenuse is the side opposite the right angle. Therefore, the sine of angle Y is given by:“`sin(Y) = YZ / ZV“`

Cosine Function

The cosine of an angle is defined as the ratio of the length of the side adjacent to the angle to the length of the hypotenuse. In a YVZ triangle, the side adjacent to angle Y is ZY. Therefore, the cosine of angle Y is given by:“`cos(Y) = ZY / ZV“`

Tangent Function

The tangent of an angle is defined as the ratio of the length of the side opposite the angle to the length of the side adjacent to the angle. In a YVZ triangle, the tangent of angle Y is given by:“`tan(Y) = YZ / ZY“`By using these trigonometric functions, we can find the measure of an angle in a YVZ triangle if we know the lengths of two sides.

For example, if we know the lengths of YZ and ZV, we can use the sine function to find the measure of angle Y:“`Y = arcsin(YZ / ZV)“`Similarly, if we know the lengths of ZY and ZV, we can use the cosine function to find the measure of angle Y:“`Y = arccos(ZY / ZV)“`Trigonometry is a powerful tool that can be used to solve a wide range of problems involving angles and triangles.

By understanding the basic principles of trigonometry, we can easily find the measure of an angle in a YVZ triangle.

Geometric Constructions

Geometric constructions are techniques used to construct geometric figures with specific properties using only a compass and a straightedge. These constructions can be applied to find the measure of angles, including angles in YVZ triangles.

Using a compass and straightedge, we can construct angles with specific measures. Here are some common geometric constructions used to find the measure of an angle:

Angle Bisector

An angle bisector is a line that divides an angle into two equal parts. To construct an angle bisector using a compass and straightedge, follow these steps:

1. Draw the angle.
2. Place the compass point at the vertex of the angle.
3. Adjust the compass to a radius greater than half the length of the longer side of the angle.
4. Draw two arcs that intersect the sides of the angle.
5. Connect the two points of intersection with a straight line.

The line drawn in step 5 is the angle bisector, and it divides the angle into two equal parts.

Perpendicular Bisector

A perpendicular bisector is a line that passes through the midpoint of a line segment and is perpendicular to it. To construct a perpendicular bisector using a compass and straightedge, follow these steps:

1. Draw the line segment.
2. Place the compass point at one endpoint of the line segment.
3. Adjust the compass to a radius greater than half the length of the line segment.
4. Draw two arcs that intersect the line segment.
5. Repeat steps 2-4 with the other endpoint of the line segment.
6. The two arcs will intersect at two points.
7. Connect the two points with a straight line.

The line drawn in step 7 is the perpendicular bisector, and it passes through the midpoint of the line segment and is perpendicular to it.

FAQ Overview

What is the angle bisector theorem?

The angle bisector theorem states that the ratio of the lengths of the two segments created by an angle bisector is equal to the ratio of the lengths of the opposite sides of the triangle.

How can I use trigonometry to find the measure of an angle?

Trigonometry provides various functions, such as sine, cosine, and tangent, which can be used to relate the lengths of sides and angles in a triangle. By applying these functions, you can determine the measure of an unknown angle.

What are some common geometric constructions used for angle measurement?

Geometric constructions such as angle bisectors, perpendicular bisectors, and compass and straightedge constructions can be employed to accurately measure angles without the need for protractors or other specialized tools.