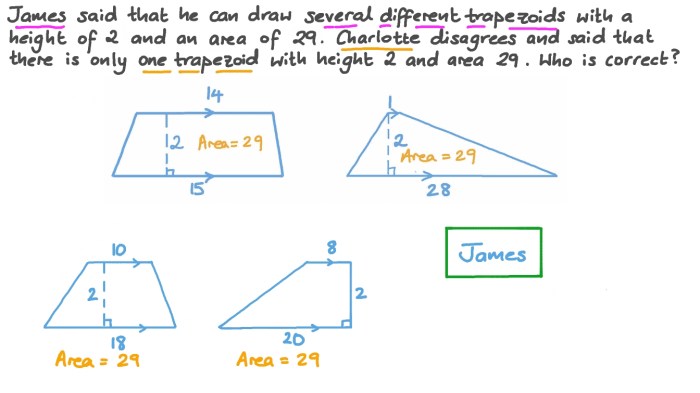
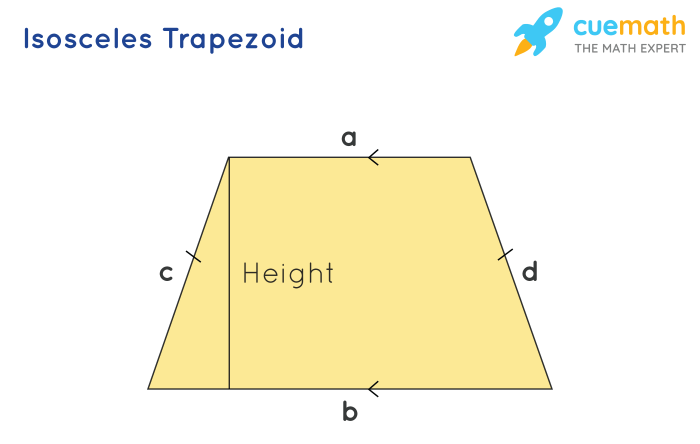
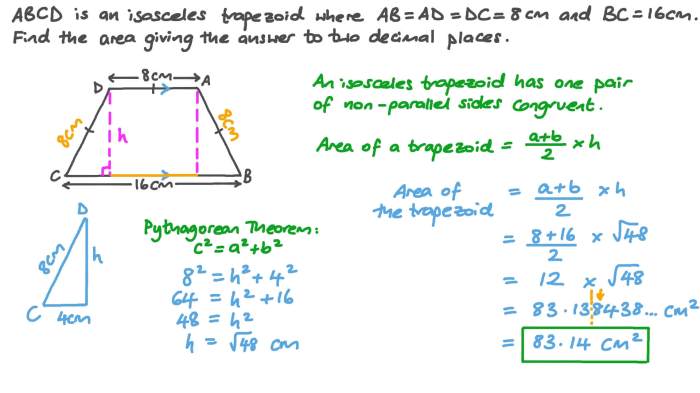
The height of a trapezoid can be expressed as x-4, a fundamental formula that unlocks a wealth of geometric insights. This equation serves as a cornerstone in various fields, empowering problem-solvers with the ability to decipher the dimensions of trapezoids with precision.
Delving into the intricacies of this formula, we embark on a journey to uncover its significance, explore its applications, and unravel common misconceptions associated with its usage.
Understanding the Trapezoid Height Formula
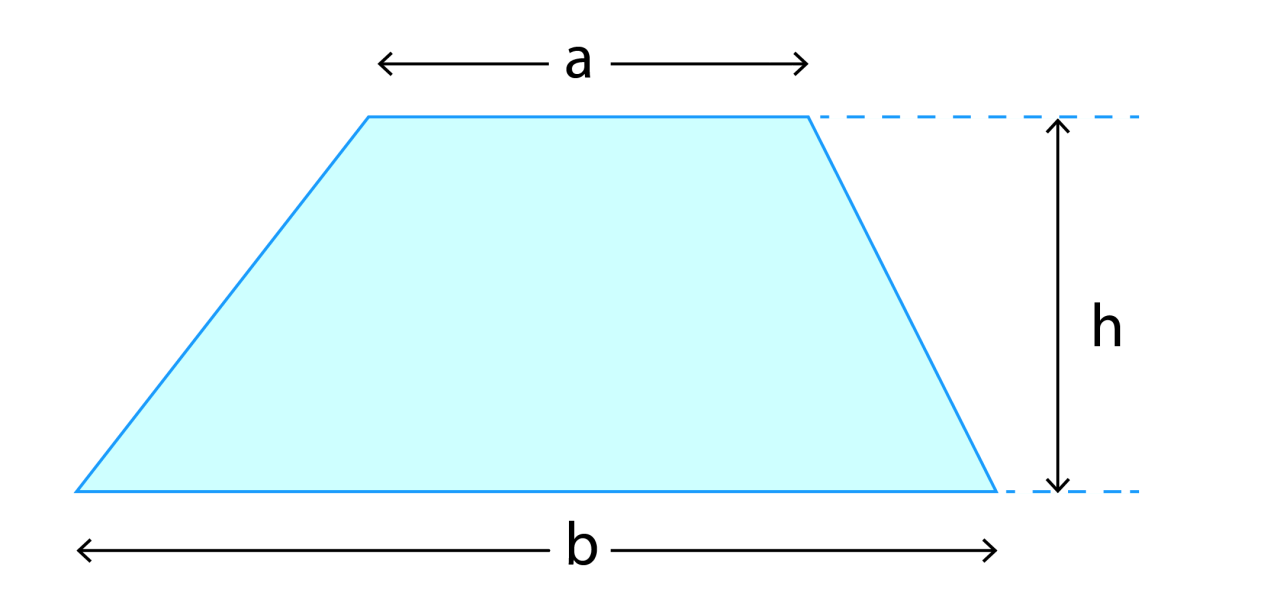
A trapezoid is a quadrilateral with two parallel sides called bases. The height of a trapezoid is the perpendicular distance between the bases. The formula “the height of a trapezoid can be expressed as x-4” is significant because it provides a method for calculating the height of a trapezoid when given certain information about its bases and height.
Methods for Calculating Trapezoid Height
- Using the formula:The formula “the height of a trapezoid can be expressed as x-4” can be used to calculate the height of a trapezoid if you know the lengths of the bases and the height. Simply plug the values into the formula and solve for x.
- Using similar triangles:If you know the lengths of the bases and the height of one of the trapezoid’s legs, you can use similar triangles to find the height of the trapezoid.
Applications of the Formula in Real-World Scenarios
The formula for calculating the height of a trapezoid is used in a variety of real-world applications, including:
- Architecture:Architects use the formula to calculate the height of windows, doors, and other openings in buildings.
- Engineering:Engineers use the formula to calculate the height of bridges, dams, and other structures.
- Design:Designers use the formula to calculate the height of furniture, appliances, and other objects.
Common Errors and Misconceptions, The height of a trapezoid can be expressed as x-4
There are a few common errors and misconceptions associated with using the formula for calculating the height of a trapezoid. These include:
- Using the wrong formula:There are different formulas for calculating the height of a trapezoid, depending on the information you have. Make sure you are using the correct formula for your situation.
- Making measurement errors:It is important to measure the bases and height of the trapezoid accurately. Even a small error in measurement can lead to a significant error in the calculated height.
Advanced Applications and Extensions
The formula for calculating the height of a trapezoid can be extended to solve more complex geometric problems. For example, it can be used to:
- Calculate the area of a trapezoid:The area of a trapezoid is equal to the product of the height and the average of the bases.
- Calculate the volume of a trapezoidal prism:The volume of a trapezoidal prism is equal to the product of the height and the area of the base.
FAQ Explained: The Height Of A Trapezoid Can Be Expressed As X-4
What is the significance of the formula “the height of a trapezoid can be expressed as x-4”?
This formula provides a direct and efficient method for calculating the height of a trapezoid, a crucial measurement in various geometric applications.
How is this formula applied in real-world scenarios?
The formula finds practical applications in fields such as architecture, where it aids in determining the height of trapezoidal roofs or windows, and engineering, where it assists in calculating the dimensions of trapezoidal beams or supports.
What are common errors to avoid when using this formula?
A common error is confusing the height of the trapezoid with its bases. It’s essential to clearly identify the height as the perpendicular distance between the parallel bases.